par De Luminae
Daylight Glare Probability (DGP)
Définition
Le DGP (Daylight Glare Probabiblity) est un indicateur d’éblouissement qui propose de quantifier le pourcentage de personnes éblouies par une scène lumineuse. Il peut être calculé par différents logiciels comme par exemple DL-Light. Les paramètres de son équation ont étés définis de façon empirique, sur la base d'études comportementales de personnes réalisant des tâches de bureautique dans un environnement éclairé par la lumière naturelle avec plusieurs types de protections solaires. Le DGP se différentie des autres indices d’éblouissement par la première moitié de son équation qui prend en compte l’éclairement vertical mesuré au niveau de l’œil et qui permet d’évaluer l’éblouissement dans des scènes peu contrastées mais très lumineuses. La seconde moitié de l’équation, plus classique, évalue les contrastes entre les sources et l’ambiance générale en tenant compte de leur luminance, leur taille, et leur position dans le champ de vision :
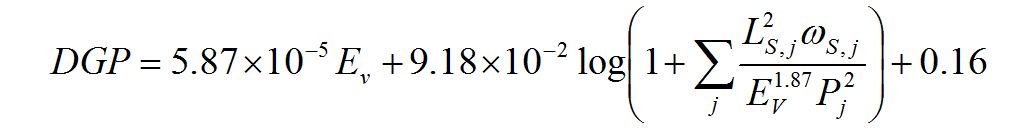
Avec :
- Ev, Eclairement vertical au niveau de l’œil (lux)
- Ls, Luminance de la source éblouissante (cd/m2)
- ωs, Angle solide de la source (sr)
- P, Index de position de la source. L’index de position P est de 1 lorsque la source est centrée dans le champ de vision et augmente à mesure que la source se rapproche de la périphérie du champ.
Caractérisation des sources d’éblouissement
Les sources potentiellement éblouissantes sont caractérisées par trois paramètres, leur luminance en cd/m2, leur taille ou angle solide exprimé en stéradian et leur position dans le champ de vision.
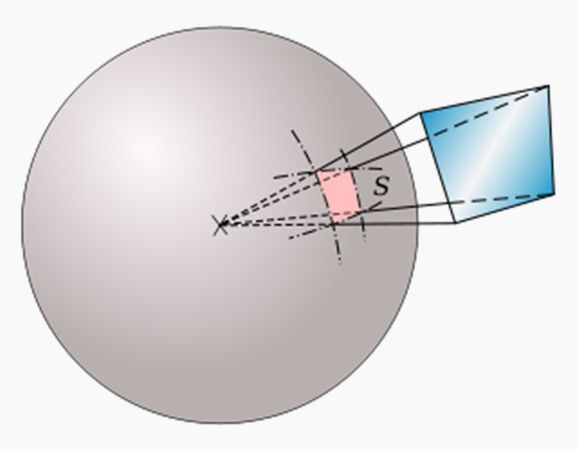
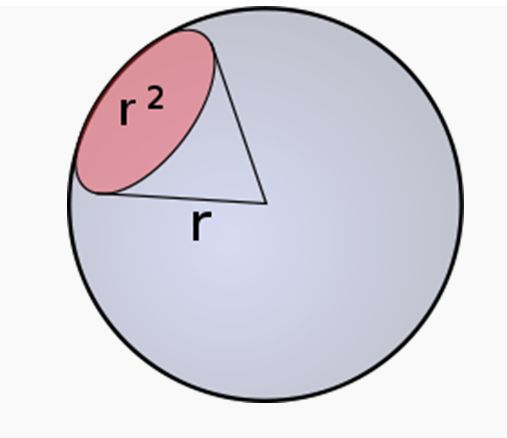
L’angle solide de la source
L'angle solide est le rapport entre la surface (en rose) de la projection d'un objet sur une sphère et le carré du rayon de la sphère. Ici, l'objet dont est mesuré l'angle solide est une surface quadrilatère (en bleu). En mathématiques, en géométrie et en physique, un angle solide est l'analogue tridimensionnel de l'angle plan ou bidimensionnel. L'angle plan étant défini, dans l'espace bidimensionnel, comme le rapport de la longueur de l'arc sur le rayon d'un cercle, l'angle solide, dans l'espace tridimensionnel, est défini de façon analogue comme le rapport de la superficie d'une partie d'une sphère sur le rayon au carré. Son unité est le stéradian noté sr.
On le note souvent Ω (oméga majuscule). Il mesure la surface sur laquelle un objet se projette radialement sur une sphère de rayon unité.
Formule usuelle
Pour calculer l'angle solide sous lequel on voit un objet à partir d'un point donné, on projette l'objet sur une sphère de rayon R centrée en ce point. Si la surface que cette projection fait sur la sphère est S, l'angle solide sous lequel l'observateur voit l'objet est, par définition :
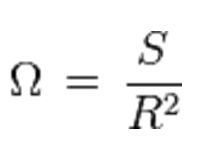
Avec :
- Ω: en stéradian (sr)
- S : en mètre carré (m2)
- R : en mètre (m)
La notion d'angle solide intervient en particulier dans la définition de la luminosité et de ses grandeurs dérivées. En général, ces grandeurs sont associées à des corps sources ou récepteurs dont les positions spatiales sont exprimées en coordonnées curvilignes (par exemple, en coordonnées sphériques : position des étoiles, satellites, capteurs au sol, etc.). On peut dès lors définir l'angle solide dans ce type de coordonnées.
Stéradian
Sa définition française officielle est: « L'unité d'angle solide est le stéradian, angle solide d'un cône qui, ayant son sommet au centre d'une sphère, découpe sur la surface de cette sphère une aire égale à celle d'un carré ayant pour côté une longueur égale au rayon de la sphère1. »
Autrement dit, un angle solide d'un stéradian délimite sur la sphère unité à partir du centre de cette sphère une surface d'aire 1. Pour une sphère complète, l'angle solide vaut donc 4π stéradians, la surface d'une sphère complète de rayon r valant 4π r2.
Exemples
- Le regard d'un œil humain embrasse environ 0,5 sr ;
- Un cône circulaire, de demi-angle au sommet θ découpe dans l'espace un angle solide de 2π (1 - cosθ). Pour faciliter ce passage du plan à l'espace, on propose une illustration. Si on met en rotation un angle plan (2θ) de 1,144 radian (65,54°) autour de sa bissectrice, il engendre un cône qui définit un angle solide de 1 stéradian.
- On peut montrer que le développement d'un cône circulaire correspondant à un stéradian fait environ 195°
L’index de position P
L’index de position P est une variable que l’on retrouve dans plusieurs indicateurs d’éblouissement (DGP, DGI, CGI, UGR). L’objectif de cet index est de tenir compte du fait qu’une même source provoque un éblouissement plus ou moins gênant suivant sa position dans le champ de vision. Une source en périphérie du champ de vision sera moins perturbante que la même source placée au centre de vision. Il existe plusieurs équations qui définissent l’indice de position.
L’index de Guth
L’index de position P définie par Guth [Luckiesh et Guth, 1949] est majoritairement utilisé. Sa définition ne le rend valable que pour des sources situées au dessus de la ligne de vue. L’étude de Luckiesh et Guth est basée sur l’appréciation de l’éblouissement perçu par 50 personnes dans des conditions bien définies d’éclairage artificiel. La première étape de l’expérience consiste à déterminer une valeur de luminance « à la limite entre le confort et l’inconfort », notée luminance BCD (between confort and disconfort), pour une petite source lumineuse placée au centre du champ de vision. La luminance BCD déterminée par l’étude est de 2843 cd/m2 c'est-à-dire pour un contraste entre la source et le fond de 1/83. Ensuite une seconde source de même taille est placée à un certain angle de la ligne de vue dans le champ visuel. Sa luminance augmente et clignote toute les secondes en alternance avec la source de luminance BCD définie auparavant et placée au centre, jusqu'à ce que la sensation d’éblouissement perçue par l’observateur soit identique pour les deux sources. L’opération est répétée pour différentes positions dans le champ de vision. L’index de position P est défini tel que la luminance d’une source en périphérie du champ de vision doit être P fois supérieure à la luminance d’une source de même taille placée au centre de vision pour provoquer la même sensation d’éblouissement. Il est donc par définition égal à 1 au centre du champ de vision. Luckiesh et Guth ont démontré que P augmente à mesure que la source s’éloigne du centre de vision quelque soit la direction choisie.
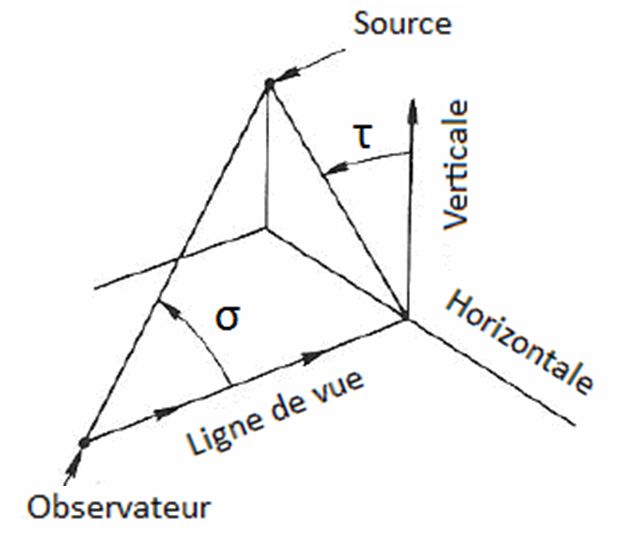
Dans le DGP, P au-dessus de la ligne de vue est définie comme suit [Wienold, 2010]:
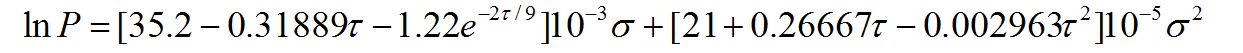
Avec :
- σ : l’angle entre la ligne de vue et la droite entre l’observateur et la source
- τ : l’angle entre le plan vertical contenant la ligne de vue et le plan contenant la ligne de vue et passant par la source.